* 이 글은 <밑바닥부터 시작하는 딥러닝2 (저자: 사이토 고키)> 책을 읽으며 정리한 글입니다.
* 나중에라도 제가 참고하기 위해 정리해 두었으며, 모든 내용을 적은 것이 아닌,
필요하다고 생각되는 부분만 추려서 정리한 것임을 미리 밝힙니다.
목차
- 퍼셉트론(perceptron)이란
- AND, NAND, OR, XOR 게이트
- 퍼셉트론의 구현
- XOR 문제
1. 퍼셉트론(perceptron)이란
퍼셉트론은 인공신경망의 아이디어를 제공한 알고리즘이다.
퍼셉트론을 요약하자면, 정보(신호)가 유효한지 아닌지 판가름하는 알고리즘이다.
내가 원하는 기준치(θ) 이상으로 정보(신호)가 세게 들어오면 '1(유효함)'을 내놓고, 그렇지 않으면 '0(유효하지 않음)'을 내놓는다. 이를 식으로 나타내면 다음과 같다.
y={0 (w1x1+w2x2≤θ)1 (w1x1+w2x2>θ)
수식 알레르기가 있는 나같은 사람을 위해 위의 수식을 그림으로 표현하자면 다음과 같다.

물론 x1과 x2뿐 아니라 x3,x4,... 등 x는 수없이 많이 늘어날 수 있다. (그에 따른 w값들도 수없이 늘어날 것이다.)
2. AND, NAND, OR, XOR 게이트
위에서, 퍼셉트론이란 정보가 유효한지 아닌지를 '판가름'하는 것이라고 했다. 즉, (명제가) 참이냐 거짓이냐를 판가름하는 것이라는 관점에서 봤을 때, 퍼셉트론은 복수의 명제가 참인지 거짓인지를 판단하는 것이라 볼 수 있다.
어떤 명제들이 어떻느냐를 판가름할 때, 여러가지 방법이 쓰인다.
복수의 명제가 모두 참일 때만 참(AND)이라고 할 수도 있고, 여러가지 중 하나만 참이어도 참(OR)이라고 결론내릴 수도 있다.
일단 모든 명제가 참일 때만 참인 경우(AND)를 살펴보자. x1과 x2에 대해 y가 어떻게 결정되는지 다음 표를 통해 나타낼 수 있다. (아래와 같이 나타내는 표를 진리표라고 한다.)
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
위의 결과들을 뒤집은 상황도 있을 수 있다. Not AND(NAND)는 AND의 모든 결과가 반대인 경우이다.
| x1 | x2 | y |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
하나의 명제만 참이어도 참인 경우(OR)를 살펴보자. x1과 x2에 대해 y가 어떻게 결정되는지 다음 표를 통해 나타낼 수 있다.
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
exclusive하게 OR인 경우도 있다. XOR이라고 한다. 즉, 한쪽만 참일때만 참인 경우이다. (형제자매가 싸울 때의 흔한 모습이다. 한 쪽이 참이면 한 쪽이 반드시 거짓이어야 상황이 말이 된다.)
| x1 | x2 | y |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
3. 퍼셉트론의 구현
x1과 x2를 넣었을 때 y가 나오는 w1과 w2, 그리고 θ는 무수히 많다.
예를 들어 AND에서, w1, w2, θ가 각각 0.5, 0.5, 0.7일 때 AND의 표를 만족하는 식을 낼 수 있다.
이것을 파이썬으로 구현하면 다음과 같이 쓸 수 있다.
def AND(x1, x2):
w1, w2, theta = .5, .5, .7
y = w1*x1 + w2*x2
if y <= theta:
return 0
elif y > theta:
return 1결과를 확인하기 위해 다음과 같은 값들을 출력해보면 된다.
AND(0,0) # 0을 출력
AND(1,0) # 0을 출력
AND(0,1) # 0을 출력
AND(1,1) # 1을 출력어찌어찌 구현은 했다만, 지금은 x1, x2만 있기에 망정이지, x1,x2,...,x100이라면 y의 식을 적는데만 한 세월일 것이다.
다행히 우리는 넘파이(numpy)라는, 아주 빠르고 효과적인 도구를 알고 있다. 좋다. 넘파이를 이용해서 y에 대한 식을 깔끔하게 정리해보자. 다만, 그 전에 우리가 알고있는 θ에 대한 식을 아주 약간만 변형할 필요가 있다.
리마인드를 위해, 우리가 일전에 작성했던 식을 가져와 보았다.
y={0 (w1x1+w2x2≤θ)1 (w1x1+w2x2>θ)
여기서, θ=−b로 놓는다면 다음과 같이 쓸 수 있다.
y={0 (b+w1x1+w2x2≤0)1 (b+w1x1+w2x2>0)
초등학교 과정을 무사히 이수했다면, 위와 같이 쓰는 것에 아무런 위화감을 느끼지 못할 것이다. (여기서 b는 bias로, '편향'이라고도 한다). 이제 고등교육과정을 이수한 사람답게 식을 써보자.
y={0 (b+∑n1wnxn≤0)1 (b+∑n1wnxn>0)
마음이 조금 편안해졌다. 이제 넘파이를 사용해 AND 게이트를 구현해보자.
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([.5, .5])
b = -.7
y = b + np.sum(w*x) # 넘파이의 위대함을 보아라!!
if y > 0:
return 1
else:
return 0이렇게 구현한 것 역시 첫번째로 구현한 결과물과 같은 결과를 보여준다.
NAND와 OR 역시 위에 구현한 것과 다르지 않게 구현된다. 가중치와 편향값만 조정하면 구현이 완료된다. NAND는 다음과 같은 가중치들을 넣으면 구현이 완성된다.
w = np.array([-.5, -.5])
b = .7OR 게이트는 다음과 같은 가중치들을 넣을 때 완성된다.
w = np.array([.5, .5])
b = -.2
4. XOR 문제
눈치 빠른 독자라면, 제시한 네 개의 진리표현(게이트) 중 하나만 쏙 빼먹었다는 사실을 알 수 있을 것이다. 바로 이 XOR 녀석이다. 이 녀석을 따로 빼놓고 'XOR 문제'라고 까지 칭하는 이유는, XOR이 다른 애들이랑은 다르게 '문제'를 일으키는 문제이기 때문이다.
이 문제를 시각화하기 위해 머리 속에 좌표평면을 그려보자. 앞서 계속 언급하고 있는 y는 결국 x1과 x2의 선형결합 형태임을 눈치 챘을 것이다. 그럼 x1과 x2가 주성분인 2차 평면을 생각해보자. OR 게이트는 시각적으로 다음과 같이 표현된다.
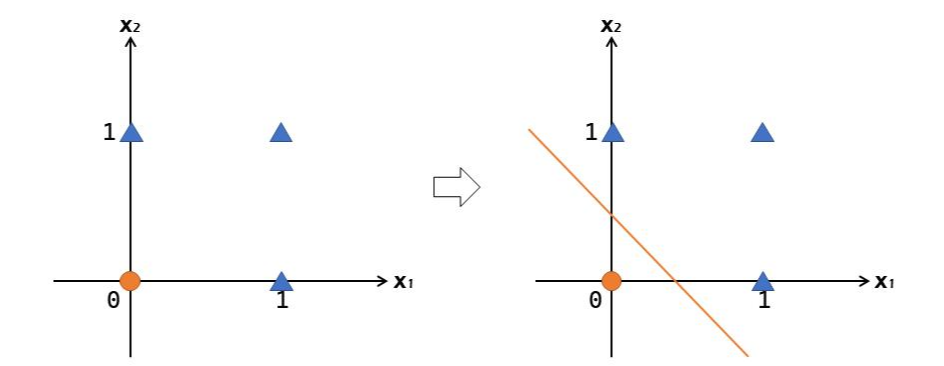
빨간 점을 제외하기 위해 단지 하나의 선만을 그어서 표현할 수 있다.
한편, XOR 게이트는 어떨까?
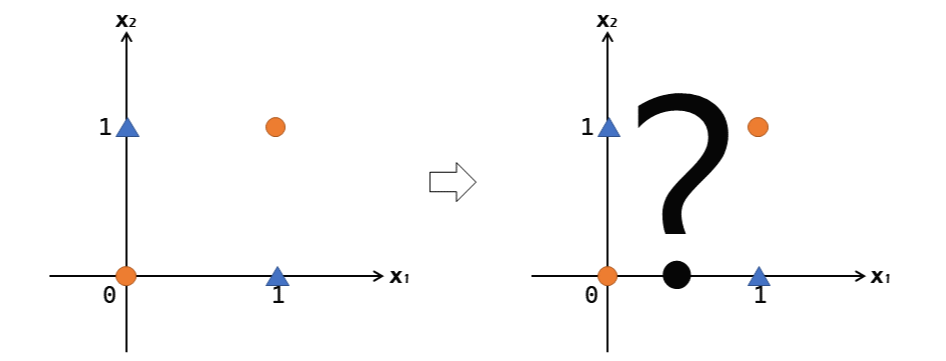
시공간의 왜곡이 일어나지 않는 한, 하나의 선으로 빨간 점들을 파란 세모들이랑 분리해낼 수는 없다.
하지만 이 문제를 풀지 못한다고 슬퍼할 필요는 없다.
우리가 지금까지 배운 것들을 잘 조합하면 이 문제를 풀 수 있기 때문이다.
XOR 문제를 풀고 싶다면 다음 포스트를 재빨리 클릭하도록 하자.
'IT Anthology > encyclopedia' 카테고리의 다른 글
| [밑러닝] 손글씨 숫자 인식으로 해보는 간단한 인공신경망 예측(feat. MNIST 데이터셋) (0) | 2020.03.17 |
|---|---|
| [밑러닝] 인공신경망 구현을 위해 알아야할 것들 (활성화 함수와 소프트맥스) (0) | 2020.03.11 |
| [밑러닝] XOR 문제의 해결, 층 쌓기 (0) | 2020.03.11 |
| [밑러닝] 1.6 matplotlib, 파이썬의 시각화 툴 (0) | 2020.02.28 |
| [밑러닝] 1.5 넘파이(numpy as np) (0) | 2020.02.28 |
