* 이 글은 <밑바닥부터 시작하는 딥러닝2 (저자: 사이토 고키)> 책을 읽으며 정리한 글입니다.
* 나중에라도 제가 참고하기 위해 정리해 두었으며, 모든 내용을 적은 것이 아닌,
필요하다고 생각되는 부분만 추려서 정리한 것임을 미리 밝힙니다.
목차
- 수치 미분(numerical differentiation)
- 기울기 벡터(gradient vector)
- 경사하강법(gradient descent method)
- 인공신경망에서의 기울기
1. 수치 미분(numerical diffrentiation)
1-(1). 수치 미분이란
미분은 고등학교 때 열심히 배웠듯이, 특정 순간의 변화량을 뜻한다. 하지만 이 '특정 순간'이라고만 하면 애매한 게, 어느 특정 순간을 콕 찝으면 사실 그 '순간'의 변화량은 측정을 할 수가 없다. 변화량이라는 것 자체가, 대상이 얼마나 변했는가를 측정해야 하기 때문에 그 순간에서 아주 조금 지난 순간까지 측정해야 변화량이란 걸 상상할 수 있는 것이다. 똑똑한 수학자들은 이것을 식으로 이렇게 표현한다.
$$
\frac {df(x)}{dx} = \lim_{h \to 0}{\frac {f(x+h)-f(x)}{h}}
$$
이와 같이, 임의 두 점에서의 함수 값들의 차이를 차분이라고 하며, 이렇게 아주 작은 차분으로 미분하는 것을 수치 미분이라고 한다. 반면 $y=x^2$을 $\frac {dy}{dx} = 2x$로 풀어내는 것과 같이, 수식을 전개해 미분하는 것을 해석적으로 미분한다고 한다.
1-(2). 수치 미분의 파이썬 구현
여기까지는 좋다. 그런데 이것을 그대로 컴퓨터로 옮기려고 하면 문제가 생긴다. h를 정말 작은 값(이를테면 $10^{-50}$)으로 설정하면 '반올림 오차'라는 문제점을 발생시키는 것이다. 이 말은, 컴퓨터가 저장하는 소수점 이하 자릿수에 한계가 있기 때문에 일정 이하의 값(소수점 8자리 이하)은 반올림하여 0.0으로 나타내는 것이다. 그럼 (1) h를 적당히 작은 값으로 합의를 보자. (2) 또한 오차를 조금이라도 높이기 위해 전방 차분(($x+h$와 $x$의 차분)이 아닌 중앙 차분 (($x+h$와 ($x-h$)의 차분)을 써보자.
위의 두 가지 개선사항을 반영하여 파이썬으로 구현하면 다음과 같다.
def numerical_diff(f,x):
h = 1e-4 # == 0.0001
return (f(x+h)-f(x-h)) / (2*h)2. 기울기 벡터(gradient vector)
지금까지 한 가지 변수에 대한 미분값에 대해 논했다. 그렇다면 두 가지 이상의 변수에 대해서는 어떻게 할까? 우리는 이미 편미분에 대해 배운 배가 있다. 함수 $f$에서 $x_0$에 대한 편미분 값을 구하려면 다른 변수는 상수 취급을 하고 $x_0$에 대해서만 미분한다. 이렇게 각 변수에 대한 편미분을 벡터로 모아놓은 것을 기울기 벡터(gradient vector) 혹은 기울기(gradient)라고 한다. 여기서는 '방향성'이 있음을 조금 더 확실히 표현하기 위해 '기울기 벡터'라고 표기하겠다.
예를 들어, $x_0 = 3$이고 $x_1 = 4$일 때, (x_0, x_1) 둘의 편미분을 묶어서 $( \frac {\partial f}{\partial x_0}, \frac {\partial f}{\partial x_1})$으로 나타낸 것이다. 이 기울기는 파이썬으로 다음과 같이 구현된다.
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x) # x와 형상이 같은 제로 배열 생성
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2)/(2*h)
x[idx] = tmp_val # 값 복원하여 다음 편미분에서 원래의 값으로 계산되도록
return grad
그렇다면 이 기울기 벡터의 크기나 방향이 의미하는 바는 무엇일까?
어떤 한 점 ($h = h(x_0,x_1)$)를 생각해보자. 이 $h$ 값이 좌표 상에서 조금 움직였을 때, 그에 따른 함수 값의 변화량이 있을 것이다. 편의상 변한만큼의 값을 $d \vec{l}$이라고 해보면, $d\vec{l} = (dx, dy)$로 나타낼 수 있다. 또한 기울기 벡터 $\nabla h$는 다음과 같이 정의된다: $\nabla h = (\frac {\partial h}{\partial x_0}, \frac {\partial h}{\partial x_1})$
한편, $h$를 편미분하는 공식은 다음과 같이 나타낼 수 있다.
$$
dh = (\frac {\partial h}{\partial x_0})dx_0 + (\frac {\partial h}{\partial x_1})dx_1
$$
이 때, 다음과 같은 값들을 알고 있다.
$$
d\vec{l} = (dx, dy) \\[3mm]
\nabla h = (\frac {\partial h}{\partial x_0}, \frac {\partial h}{\partial x_1})
$$
따라서 $dh$는 다음과 같이 나타낼 수 있다.
$$
dh = \nabla h \cdot d \vec{l}
$$
여기서, $dh$를 최대로 하기 위해서는 $\nabla h$와 $d \vec{l})$가 같은 방향으로 나란해야 한다. (둘이 직교하면 $dh$는 0이 되고, 이것을 따라가다 보면 등고선을 그릴 수 있다. 다만 실제 머신러닝의 과제에서는 이렇게 완벽하게 함수를 그리고 시작하는 경우가 드물어서, 기울기 벡터를 단서 삼아 최저점을 더듬더듬 찾아가야 한다.)
위키백과에서 찾아보면, 기울기 벡터(gradient vector)가 의미하는 바는 다음과 같다.
"direction and rate of fastest increase"
이해를 돕기 위해 시각화를 해보자. $f(x_0, x_1) = x_0^2+ x_1^2$ 그래프를 그려보면 다음과 같다.
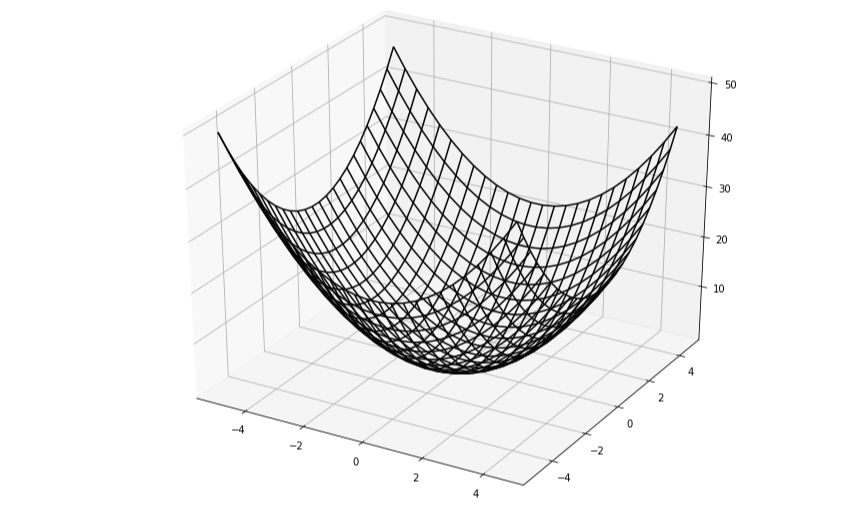
이에 대한 기울기 벡터를 구하여 그래프로 나타내면 다음과 같다.
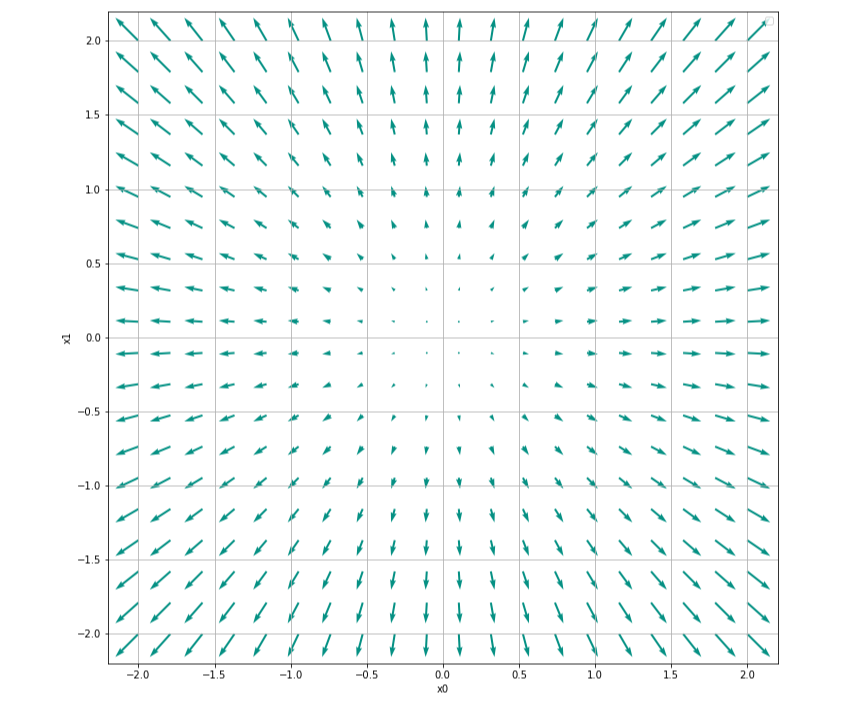
위의 3d 그래프와 번갈아 보면, 기울기 벡터는 증가하는 방향을 향해 화살표가 뻗어있으며, 변화가 급격할수록 기울기 벡터의 화살표가 더 길어지는 것을 볼 수 있다.
그렇다면 $f(x_0, x_1) = \sin (x_0)+ \sin (x_1)$일 때, $f(x_0, x_1)$의 기울기 그래프를 보고 $f(x_0, x_1)$ 그래프가 어떤 모양인지 감을 잡아보자.

왼쪽 하단에 있는 점에서 다른 네개의 지점을 향해 뻗어나가고, 오른쪽 상단의 점에서 대부분의 화살표의 방향이 수렴한다. 왼쪽 하단이 제일 낮고, 오른쪽 상단으로 갈수록 제일 빠르게 증가하는 기울기를 가지고 있을 것이라 예측할 수 있다.
실제 $f(x_0, x_1)$ 그래프는 3차원에서 아래와 같이 그려진다.
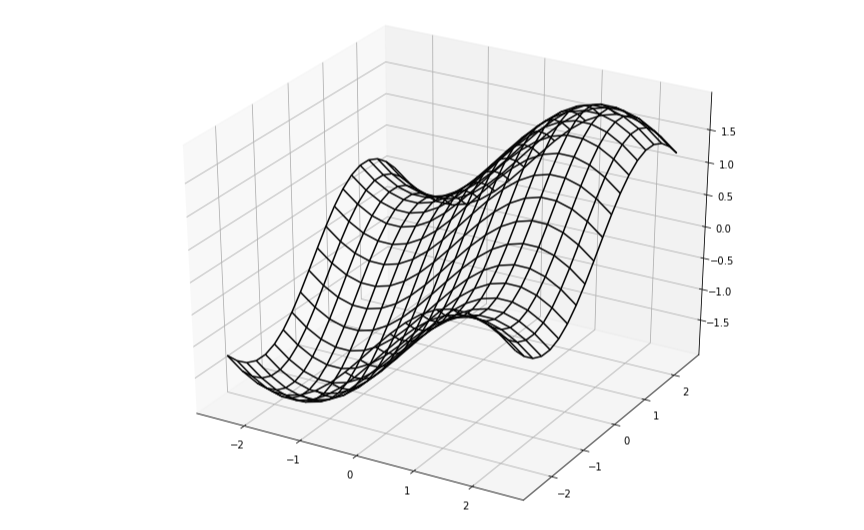
머신러닝에서는 최저점을 찾아내야하기 때문에 위에 그렸던 화살표들의 반대 방향, 즉 기울기가 가장 빠르게 감소하는 방향으로 탐색을 한다.
3. 경사하강법(gradient descent method)
여기서 경사법은 기울기가 가리키는 방향으로 가서, 거기서 다시 기울기를 구하는 행위를 반복하는 것이다. 이렇게 최솟값을 찾도록 노력하는 방법을 '경사법(gradient method)'이라고 한다. 이 중에서 함수의 값이 하강하는 방향으로 가도록 하는 것을 '경사하강법'이라고 한다.
경사법을 수식으로 나타내면 다음과 같다.
$$
x_0 = x_0 - \eta \frac {\partial f}{\partial x_0} \\[3mm]
x_1 = x_1 - \eta \frac {\partial f}{\partial x_1}
$$
여기서 $\eta$는 학습률(learning rate)로, 어느 정도의 비율로 값을 갱신할 것인지 정해주는 용도이다. 위의 단계를 반복하면 서서히 함수값이 낮은 곳을 향해 갱신된다. (엄밀히 따지면 위의 수식은 수학적으로는 맞지 않다. 양변이 전혀 같지 않기 때문이다. 등호(=)보다는 화살표($\gets$)같은 것을 이용해서 표시해도 되지만, 파이썬 코드로 옮길 때는 전혀 이질감이 없기 때문에 그냥 표기하겠다.)
경사하강법을 파이썬으로 구현하면 다음과 같다.
def gradient_descent(f, init_x, lr = 0.01, step = 100):
x = init_x
for i in range(step):
grad = numerical_gradient(f, x)
x -= lr * grad
return x즉, 정해진 step만큼 반복하며 기울기에 학습률 lr을 곱한 만큼씩 나아가는 것이다.
4. 인공신경망에서의 기울기
지금까지 gradient에 대해 열심히 배웠다. 그렇다면 이게 머신러닝에서 어떻게 쓰이기에 이다지도 열심히 배운 것일까?
머신러닝에서는 실제 답과 예측한 값의 차이를 나타내는 '손실 함수'가 있고, 이 손실 값(쉽게 생각하면 실제 답과 예측 값의 차이)이 낮아질수록, 예측 값은 실제 답과 근접한다. 따라서 손실 함수의 최저값을 찾아가는 것이 인공신경망이 해야할 일이라는 뜻이다.
실제의 머신러닝 과제에서 손실 함수는 복잡다단하며 한번에 쨘 나타내기 어렵기 때문에, 해석학적으로 미분하여 기울기 값을 구하는 것보다 수치 미분법으로 기울기를 구해, 함수의 최솟값을 찾아 나가는 것이 타당하다.
정리
지금까지 수치 미분과 기울기 벡터 계산, 경사하강법에 대해서 살펴보았다. 앞서 잠깐 얘기했듯이,
다음 포스트에서는 신경망의 학습 알고리즘을 (드디어!) 구현해보도록 하자.
'IT Anthology > encyclopedia' 카테고리의 다른 글
| [밑러닝] 이보다 더 쉬울 수는 없다! 오차역전파(back-propagation)법 완벽 파헤치기 (0) | 2020.03.29 |
|---|---|
| [밑러닝] 밑바닥부터 구현하는 인공신경망 학습 알고리즘 (0) | 2020.03.29 |
| [밑러닝] 인공신경망의 학습 지표, 손실함수(loss function) (0) | 2020.03.17 |
| [밑러닝] 손글씨 숫자 인식으로 해보는 간단한 인공신경망 예측(feat. MNIST 데이터셋) (0) | 2020.03.17 |
| [밑러닝] 인공신경망 구현을 위해 알아야할 것들 (활성화 함수와 소프트맥스) (0) | 2020.03.11 |
